Vamos a sumar las matrices A y B:
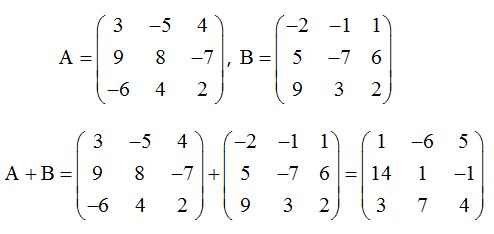
♣Restar matrices♣
Es lo mismo que en el caso anterior pero restando los valores que ocupan las mismas posiciones:
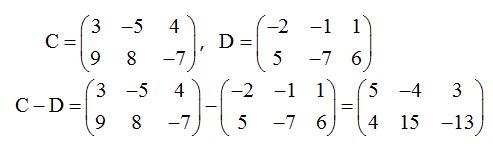
♣Multiplicar matrices♣
Vamos a considerar 2 casos:
1) Multiplicar una matriz por un escalar
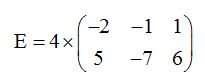
Multiplicamos cada elemento por el escalar:
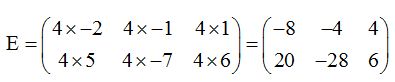
2) Multiplicar dos matrices es preciso que la 1ª tenga tantas columnas como filas la 2ª matriz. El resultado será una matriz que tiene el mismo número de filas como tiene la 1ª y tantas columnas como tiene la 2ª:
Multiplicamos las matrices:
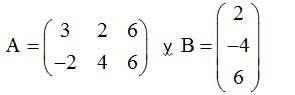
Tenemos que multiplicar el primer elemento de la 1ª fila de A (3) por el primer elemento de la fila de B (2).
El segundo elemento de la fila 1ª de A (2) por el 2º elemento de la fila de B (-4).
El tercer elemento de la 1ª fila de A (6) por el tercer elemento de la fila de B (6).
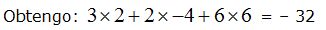
Hago lo mismo con los elementos de la 2º fila de A:
Multiplico el primer elemento de la 2ª fila de A (– 2) por el primer elemento de la fila de B (2).
El segundo elemento de la fila 2ª de A (4) por el 2º elemento de la fila de B (-4).
El tercer elemento de la 2ª fila de A (6) por el tercer elemento de la fila de B (6).
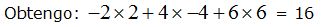
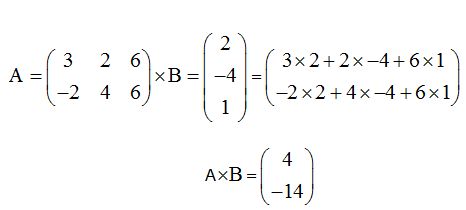
No hay comentarios:
Publicar un comentario