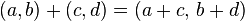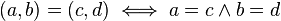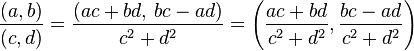AlgeLine: agosto 2015

1.2 Operaciones fundamentales con números complejos.

Adicción

Dados los complejos Z1 = (a;b) y Z2 = (c ;d). Se define Z1 + Z2 = (a; b) + (c; d) = (a +c; b+ d)

Sustracción

Se obtiene sumando al minuendo el opuesto del sustraendo : Z1 + (-22) = (a; b) + (-c ; d) = (a – c ; b-d)

Multiplicación

Dados los complejos Z1 = (a ; b) y Z2 = (c ; d), se define Z1 * Z2 = (a*c-b*d; a*d + b*c)

Potenciación

La potenciacion de un numero complejo con potencia natural, se resuelve como una multiplicacion reiterada: Zn = (a ; b)n = (a ;b)1.(a ; b)2……(a ; b)n asociado de a dos pares los pares ordenados.

Forma Binomica

La forma Binomica de un numero complejo es: Z = a + bi

Operaciones de números complejos en su forma Binomica: La suma y diferencia de numeros complejos se realiza sumando y restando partes reales entre si y partes imaginarias entre si.

+(a +bi) + (c + di) = (a+c) + (b+d) i

-(a +bi) - (c + di) = (a-c) + (b-d) i

Multiplicación con números complejos

El producto de los números complejos se realiza aplicando la propiedad distributiva del producto respecto de la suma y teniendo en cuenta que i2 = -1 (a + bi) – (c + di) = (ac-bd) + (ad + bc) i

División con números complejos

El cociente de números complejos se hace racionalizando el denominador; esto es, multiplicando numerador y denominador por el conjugado de este.

Ejemplo

(3 + 2i) + 8-7-i) = (3-7) + (2i – i) = -4 + i

= (5 + 3i) + {(-1 + 2i) + (7-5i)}

=(5 + 3i) + {(-1 + 7) + (2i – 5i)}

= (5 + 3i) + (6 – 3i)

= (5 + 6) + (3i – 3i)

= 11

1.1.- Definición y origen de los números complejos.

Los números complejos son una extensión de los números reales y forman el mínimo cuerpo algebraicamente cerrad oque los contiene. El conjunto de los números complejos se designa con la notación

\scriptstyle \mathbb{C}

, siendo

\scriptstyle \mathbb{R}

el conjunto de los números reales se cumple que

\scriptstyle \mathbb{R}\sub\mathbb{C}

Los números complejos incluyen todas las raíces de lospolinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y unnúmero imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i), o en forma polar.

Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, facilitación de cálculo de integrales, en aerodinámica, hidrodinámica y electromagnetismo entre otras de gran importancia.

Suma

(a, b) + (c, d) = (a+c,\, b+d)

Producto por escalar

r(a, b) = (ra,\, rb)

Multiplicación

(a, b) \cdot (c, d) = (ac - bd, ad + bc)

Igualdad

(a, b) = (c, d) \iff a = c \and b = d

A partir de estas operaciones podemos deducir otras como las siguientes:

Resta

(a, b) - (c, d) = (a-c,\, b-d)

División

\frac{(a, b)}{(c, d)} = {(ac+bd,\,bc-ad) \over c^2+d^2} = \left({ac + bd \over c^2 + d^2} , {bc - ad \over c^2 + d^2}\right)

Unidad I.- Números Complejos

1.1.- Definición y origen de los números complejos. 1.2.- Operaciones fundamentales con números complejos. 1.3.- Potencias de "i", módulo o valor absoluto e un número complejo. 1.4.- Forma polar y exponencial de un número complejo. 1.5.- Teorema de Moivre, potencias y extracciones de raíces de un número complejo. 1.6.- Ecuaciones polinómicas.